Table of Contents
SFD and BMD
Shear Force:
It is the algebraic sum of the vertical forces acting to the left or right of the cut section
Bending Moment:
It is the algebraic sum of the moment of the forces to the left or to the right of the section taken about the section
Objectives
When a beam is loaded by forces or couples, stresses and strains are created throughout the interior of the beam.
To determine these stresses and strains, the internal forces and internal couples that act on the cross sections of the beam must be found.
Beams
Members that are slender and support loads applied perpendicular to their longitudinal axis.
Internal Reactions in Beams
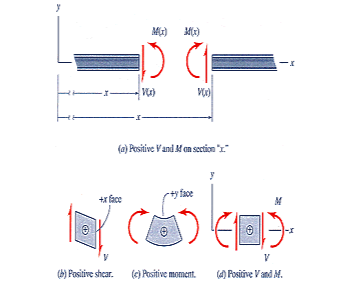
At any cut in a beam, there are 3 possible internal reactions required for equilibrium:
- normal force,
- shear force,
- bending moment.
Sign Conventions
Finding Internal Reactions
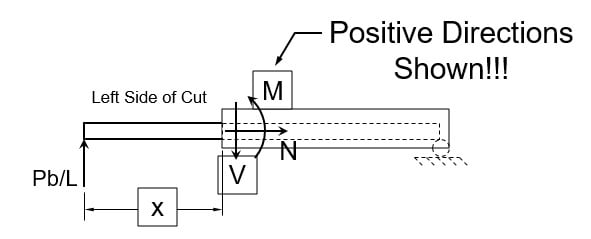
- Pick left side of the cut:
- Find the sum of all the vertical forces to the left of the cut, including V. Solve for shear, V.
- Find the sum of all the horizontal forces to the left of the cut, including N. Solve for axial force, N. It’s usually, but not always, 0.
- Sum the moments of all the forces to the left of the cut about the point of the cut. Include M. Solve for bending moment, M
- Pick the right side of the cut:
- Same as above, except to the right of the cut.
Practical Example
Find the internal reactions at points indicated. All axial force reactions are zero. Points are 2-ft apart.


Draw Some Conclusions
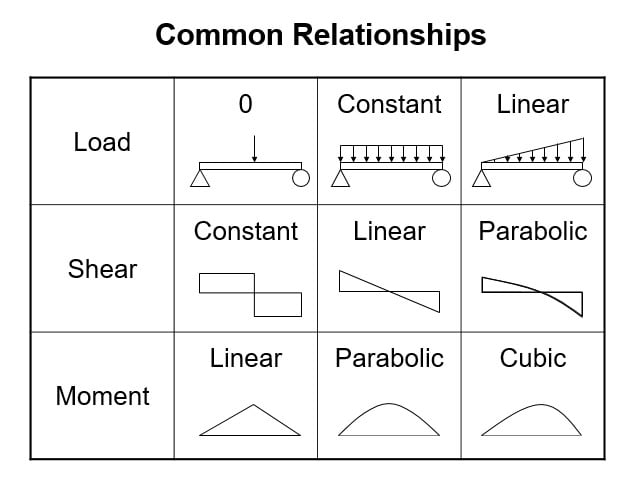
- The magnitude of the shear at a point equals the slope of the moment diagram at that point.
- The area under the shear diagram between two points equals the change in moments between those two points.
- At points where the shear is zero, the moment is a local maximum or minimum.