Table of Contents
Statement:
To determine tension in various points of a hanging rope loaded at different Points.
Purpose:
To compare the experimental and theoretical results of flexible rope system
Apparatus:
- Flexible Hanging Rope
- Spring Balances
- Weights and-Hangers.
- Meter rod and Measuring Tapes
Related Theory:
Force:
“Action of one body on another is called force.”
Units: –
SI units of force are Newton (N).
FPS units of force are pound (lbs).
Equilibrium:
A body is said to be in equilibrium if all the forces and moments applied on it are In balanced –Condition.
Conditions of Equilibrium:
There are three conditions of Static equilibrium.
Ʃ Fx = 0, Ʃ Fy = 0, Ʃ M = 0
Concurrent force System:
“A system of forces in which all these forces are passing ‘through same point is called. concurrent force system.”
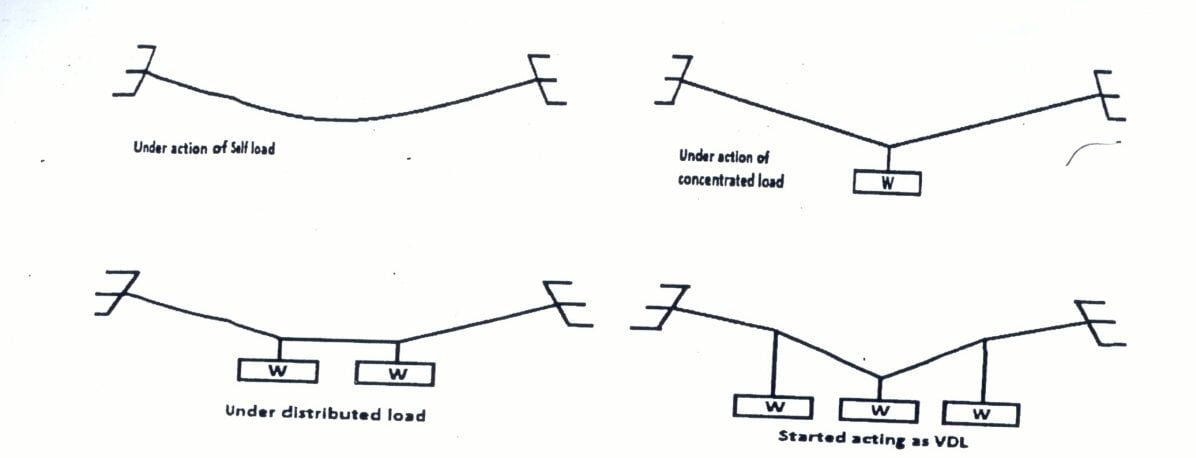
Flexible. Rope Structure:
In design of these structures it is important to know the relation involving ‘tension, span, sag, and length of cables.
These are determined by considering the cable as a body in equilibrium. In analysis of flexible cables it is assumed that any resistance offered to bending is negligible. This assumption means that the force in the cable will be along the length of the cable i.e. only tensile force
Behavior of flexible Cable:
Procedure:
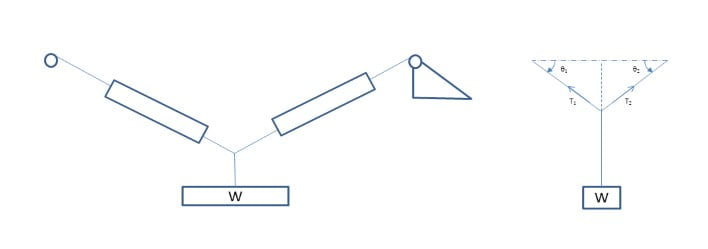
- Note down the initial reading of two spring balances, as zero error
- Add weight (W) to the hanger and note the readings on both spring balances
- Value of T1 and T 2 may be deduced by subtracting zero error from the second reading
- Repeat the experiment at least four times by changing weight and take corresponding readings
- Calculate the analytical results with the help of two conditions of equilibrium:
- Ʃ Fx = 0,
a) T 2 Cosθ2 – T1Cos θ1 = 0
T 2 = T 1(Cosθ1/Cos θ2——————————- (1)
b) Ʃ Fy = 0,
T1 Sin θ1+ T2 Sin θ2 = W
T1 Sin θ1 + T1 Sin θ2( Cos θ1)/ Cos θ2 = W
T1 (Sin θ1 + Tan θ2 Cosθ2) = W
T1 = W/ (Sinθ1 + Tanθ2 Cos θ1) ———————– (2)
Observations and Calculations
| Height (in) | W | L 1(in) | L 2 (in) | Θ 1 | Θ 2 | T 1 (lb) | T 2 (lb) | |||||
| Zero Error = | Zero Error = | |||||||||||
| N | lb | Exp | Anal | % Diff | Exp | Anal | % Diff | |||||
| 1 | ||||||||||||
| 1 | ||||||||||||
| 1 | ||||||||||||
| 1 | ||||||||||||
Note: the difference between experimental and analytical values of tension should not be more than 10%, if so that reading may be discarded
Precautions
- All the distances should be measured properly.
- Both pulleys should be frictionless.
- While noting down the reading, spring balances should not be firmly gripped in the hands.