Analysis Of Trusses By Method Of Joints

Author: Farhan Khan
Posted On: April 29, 2020
Updated On: April 29, 2020

The method of joints is one of the simplest methods for determining the force acting on the individual members of a truss because it only involves two force equilibrium equations. Since only two equations are involved, only two unknowns can be solved for at a time.

Therefore, you need to solve the joints in a certain order. That is, you need to work from the sides towards the center of the truss. When a force points toward the joint, the member is said to be in compression. If the force points away from the joint, the member is said to be in tension. It is often important to know whether a truss member is in tension or in compression because some building materials have different strengths in compression versus tension.

Table of Contents

Principle

If a truss is in equilibrium, then each of its joints must also be in equilibrium.
The method of joints consists of satisfying the equilibrium equation for forces acting on each joint.
∑Fx = 0 ∑Fy = 0
Recall, that the line of action of a force acting on a joint is determined by the geometry of the truss member.
The line of action is formed by connecting the two ends of each member with a straight line.
Since direction of the force is known, the remaining unknown is the magnitude of the force.

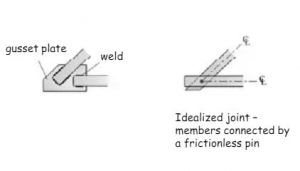
Procedure

If possible, determine the support reactions
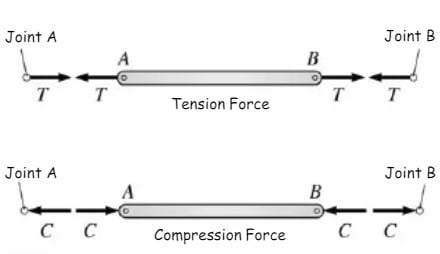
Draw the free body diagram for each joint. In general, assume all the force member reactions are tension (this is not a rule, however, it is helpful in keeping track of tension and compression members).
Write the equations of equilibrium for each joint,

∑Fx = 0 ∑Fy = 0
If possible, begin solving the equilibrium equations at a joint where only two unknown reactions exist.

Work your way from joint to joint, selecting the new joint using the criterion of two unknown reactions.
Solve the joint equations of equilibrium simultaneously.

Tips

The joints with external supports always connect with two truss members.
Thus many times, the analysis starts from analyzing the supports.
Therefore very often the analysis begins with finding the reaction forces applied at the supports.
Pay attention to symmetric systems and zero force members.
Identification of these special cases sometimes will make the whole analysis way easier.

Zero Force Members

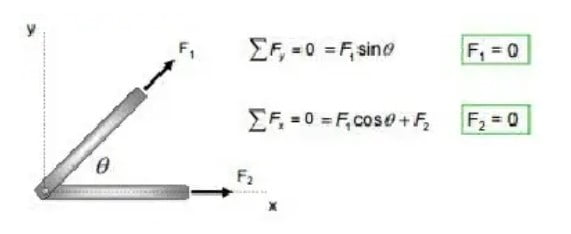
Truss analysis may be simplified by determining members with no loading or zero force.These members may provide stability or be useful if the loading changes zero-force members may be determined by inspection of the joints

Case 1

If two members are connected at a joint and there is no external force applied to the joint.

Case 2

If three members are connected at a joint and there is no external force applied to the joint and two of the members are collinear.

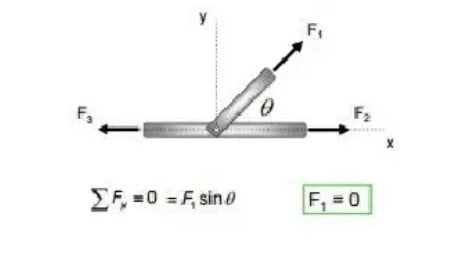
Practical Example

Since direction of the force is known, the remaining unknown is the magnitude of the force.

Step 1 (Free body Diagram)

Free-body diagram of entire truss. Calculating the reactions is a good place to start because they are usually easy to compute, and they can be used in the equilibrium equations for the joints where the reactions act.

Step 2 (Equation of Equilibrium)

Equilibrium equations for entire truss

Step 3

Free body diagram of Joint C

Step 4

Equilibrium equations for joint C. It is a good idea to assume all members in tension (forces point away from the joint, not towards it). Then, after solving the equilibrium equations, you will know immediately that any member force found to be negative must be compression.

Step 5

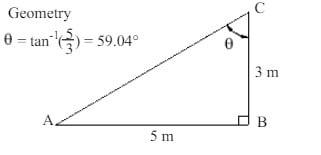
Step 6 (Trigonometry)

Using Angle= 59.04° in Eqs. 4 and 5 and solving simultaneously gives

Writing “(T)” after the numerical value shows that the member is in tension. We had arbitrarily assumed member BC to be in tension. We then found that the member force was negative, so we know that our assumption was wrong. Member BC is in compression, and we show this by writing a positive “6.0” followed by “(C)”

Step 7

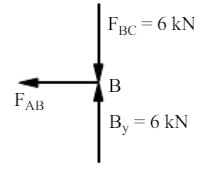
Free body diagram of joint B

Step 8

The force F BC is directed toward the joint because member BC is known to be in compression.

Step 9

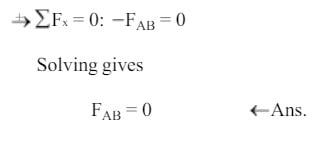
Equilibrium equation for joint B

Step 10 (Final Result)

An “Answer diagram” summarizes the analysis of the entire truss (All forces are in kN)

Author: Farhan Khan

Farhan is a highly experienced civil engineer from the Southern side of Texas and has been associated with ConstructionHow since 2020. Over almost a decade, his wide span of expertise enabled him to bring forth his fair share of stories and experiences related to the most iconic engineering examples worldwide. He has also contributed to online and offline publications on requests. Engineering is his passion, which is why he chose to become part of our honorable team of industry experts looking to provide authentic and credible guidelines to the reader.