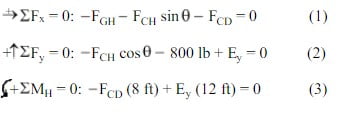If only a few of the member forces are of interest, and those members happen to be somewhere in the middle of the truss, it would be very inefficient to use the method of joints to solve for them. In such cases, method of sections is used. In the method of joints, we are dealing with static equilibrium at a point. This limits the static equilibrium equations to just the two force equations.
A section has finite size and this means you can also use moment equations to solve the problem. This allows solving for up to three unknown forces at a time.
Since the method of sections allows solving for up to three unknown forces at a time, you should choose sections that involve cutting through no more than three members at a time.
Table of Contents
Principle
If a truss is in equilibrium, then whichever section of the truss being considered must also be in equilibrium.
The Method of Sections involves analytically cutting the truss into sections and solving for static equilibrium for each section. The sections are obtained by cutting through some of the members of the truss to expose the force inside the members.
Since truss members are subjected to only tensile or compressive forces along their length, the internal forces at the cut member will also be either tensile or compressive with the same magnitude. This result is based on the equilibrium principle and Newton’s third law.
Procedure for Analysis
- Decide how you need to “cut” the truss. This is based on: a) where you need to determine forces, and, b) where the total number of unknowns does not exceed three (in general).
- Decide which side of the cut truss will be easier to work with (minimize the number of reactions you have to find).
- If required, determine the necessary support reactions by drawing the FBD of the entire truss and applying the equations of equilibrium (E-of-E).
- Draw the FBD of the selected part of the cut truss.
- We need to indicate the unknown forces at the cut members. Initially we may assume all the members are in tension, as we did when using the method of joints.
- Upon solving, if the answer is positive, the member is in tension as per our assumption. If the answer is negative, the member must be in compression. (Please note that you can also assume forces to be either tension or compression by inspection as was done in the figures above.)
- Apply the E-of-E to the selected cut section of the truss to solve for the unknown member forces. Please note that in most cases it is possible to write one equation to solve for one unknown directly.
Steps involved in Method of Sections
Step 1:
Identify the section 1-1 which passes through the members whose forces are required and note that the section is not passing through more than three members. For example, to find force in members FH and GI consider the section 1-1 as shown.
Using equations of equilibrium, find the reactions (VA, HA and VL)
Step 2:
Using this section 1-1, separate the truss into two parts. The free body diagram of
both the parts is drawn.
One of the two parts of the truss obtained after the intersected members have been cut
may be used as free body
Step 3:
Select the portion of free body where the member of forces are minimum. Hence the right part of free body is selected as it involves five forces only (PHF, PIF, PIG, VL and F4). But the left part involves eight forces (VA, HA,F1, F2, F3, PFH, PFI,PGI). Assume all the member forces are tensile.
Step 4:
Use the equations of equilibrium ΣFx = 0 : ΣFy = 0 and ΣM = 0 and find forces in members HF, FI, and CI. If positive values are obtained, the members are in tension. If the force in member becomes negative, the nature of force assumed is not correct. Hence it is modified to be compression. These steps are illustrated in numerical examples.
Tips
About the sense of forces, you can always choose to draw an unknown force as tension. Then if it comes out minus I know it is compression. This is common practice but not the eleventh commandment.
Practical Example
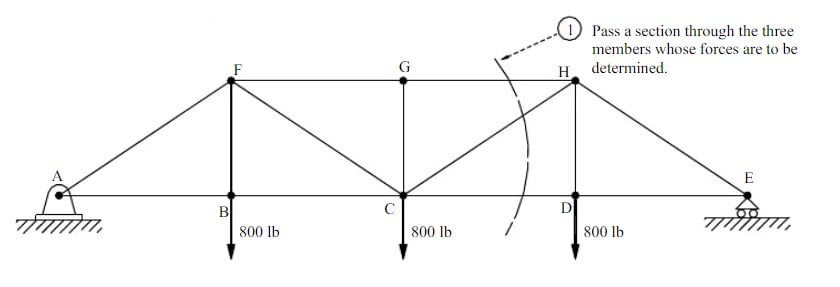
Determine the force in members CD, CH, and GH, and state whether the force is tension or compression.
Step 1 (Cutting the Section)
Cut the sections in which you want to find the forces.
Step 2
Free-body diagram of portion of truss to right of section
Step 3
At each cut through a member, a force is shown Their direction helps us find the forces.
Step 4 (Equilibrium Equations)
Equations of equilibrium for the portion of the truss:
Three equations but four unknown so another equation is needed.
Step 5 (Trigonometry)
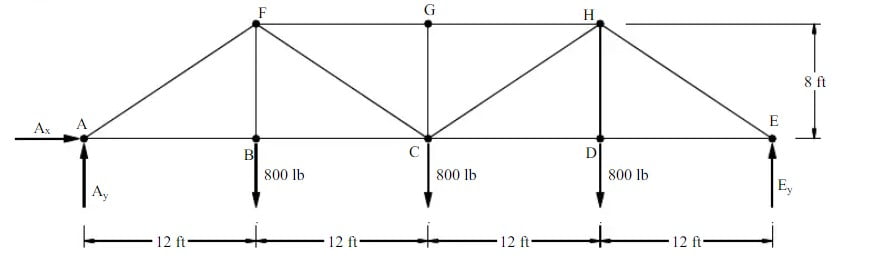
Step 6 (FBD)
Free-body diagram of entire truss
Step 7 (Fourth Equation)
Equilibrium equation for entire truss. This will give the needed fourth equation.
Step 8 (Final Result)