Table of Contents
Background
- The problem in increasing the capacity of the beam is the restriction that As should not exceed Asmax. This places a restriction on the maximum flexural capacity of the beam.
- If As exceeds Asmax, the strain in concrete will reach to a value of 0.003 before εs reaches to 0.005, thus violating the ACI code recommenation for ensuring ductile behavior.
- However, If either the strength of concrete is increased or some reinforcement is placed on compression side, the load at which strain will reach to a value of 0.003 will be increased, When this happens As on tension side can be increaseed without compromising ductility, which will also increase the flexural capacity of the beam.
- Practically this can achieved simply by placing some amount of additional reinforcement As′ on both faces (tension and compression) of the beam. This will increase the range of Asmax
- In this case the beam is called as doubly reinforced beam.
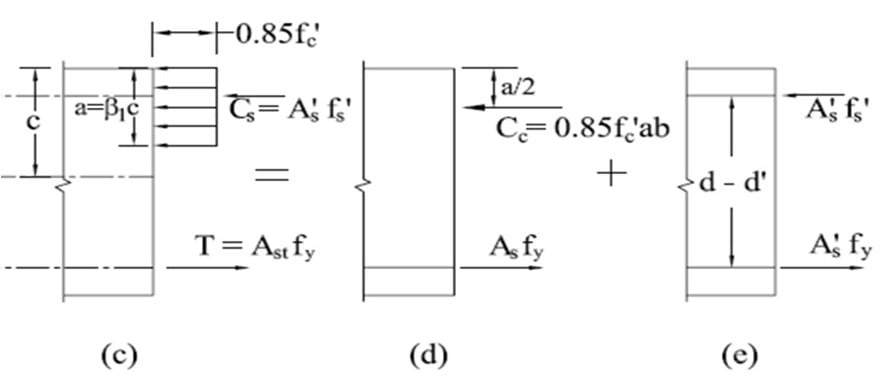
Flexural Capacity
- Consider figure d and e, the flexural capacity of doubly reinforced beam consists of two couples:
- The forces Asfy and 0.85fc′ab provides the couple with lever arm (d – a/2).
- Mn1 = Asfy (d – a/2) (c)
- The forces As′fy and As′fs′ provide another couple with lever arm (d – d′).
- Mn2 = As′fs′ (d – d′) (d)
The total nominal capacity of doubly reinforced beam is therefore,
Mn = Mn1 + Mn2 = Asfy (d – a/2) + As′fs′ (d – d′)
Factored flexural capacity is given as,
ΦMn = ΦAsfy (d – a/2) + ΦAs′fs′ (d – d′) (e)
Avoid failure, ΦMn ≥ Mu. For ΦMn = Mu, we have from equation (e), Mu = ΦAsfy (d – a/2) + ΦAs′fs′ (d – d′) (f)
Where, ΦAsfy (d – a/2) is equal to ΦMnmax (singly) for As = Asmax
Therefore, Mu = ΦMnmax (singly) + ΦAs′fs′ (d – d′)
{Mu – ΦMnmax (singly)} = ΦAs′fs′ (d – d′)
As′ = {Mu – ΦMnmax (singly)}/ {Φfs′ (d – d′)} ……….……. (g) ; where, fs′ ≤ fy
Maximum Reinforcement
Cc + Cs = T [ ∑Fx = 0 ]
0.85fc′ab + As′fs′ = Astfy
For Amax = β1c = 0.85 × 0.375d; Ast will become Astmax
0.85fc′β10.375db + As′fs′ = Astmaxfy
Astmax = β10.31875bdfc′/fy + As′fs′/fy
Astmax = Asmax (singly) + As′fs′/fy
Cc = Compression force due to concrete in compression region,
Cs = Compression force in steel in compression region needed to
balance the tension force in addition to the tension force provided by Asmax (singly).
- Astmax = Asmax (singly) + As′fs′/fy
- The total steel area actually provided Ast as tension reinforcement must be less than Astmax in above equation i.e. Ast ≤ Astmax
- Astmax (singly ) is a fixed number, whereas As′ is steel area actually placed on compression side. (For more clarification, see example)
- Note that Compression steel in the above equation may or may not yield when tension steel yields.
Conditions at which fs′ = fy when tension steel yields.
- By similarity of triangle (fig b), compression steel strain (εs′) is,
- εs′ = εu (c – d′)/ c (h)
- For tensile steel strain (εs) = εt = 0.005 (for under reinforced behavior):
- c = 0.375d
- Substituting the value of c in eqn. (h), we get,
- εs′ = εu (0.375d – d′)/ 0.375d = (0.003 – 0.008d′/d) (i)
- Equation (i) gives the value of εs′ for the condition at which reinforcement on tension side is at strain of 0.005 ensuring ductility.
Conditions at which fs′ = fy when tension steel yields.
- εs′ = {0.003 – 0.008d′/d} ……..……………….. (i) OR
- d′/d = (0.003 – εs′)/0.008 (j)
- Substituting εs′ = εy,in equation (j).
- d′/d = (0.003 – εy)/0.008 (k)
- Equation (k) gives the value of d′/d that ensures that when tension steel is at a strain of 0.005 (ensuring ductility), the compression steel will also be at yield.
- Therefore for compression to yield, d′/d should be less than the value given by equation (k).
Conditions at which fs′ = fy when tension steel yields.
- Table 3 gives the ratios (d′/d) and minimum beam effective depths (d) for compression reinforcement to yield.
- For grade 40 steel, the minimum depth of beam to ensure that compression steel will also yields at failure is 12.3 inch.
| Table 3: Minimum beam depths for compression reinforcement to yield | ||
| fy, psi | Maximum d’/d | Minimum d for d’ = 2.5″ (in.) |
| 40000 | 0.2 | 12.3 |
| 60000 | 0.12 | 21.5 |
Design Steps
- Step No. 01: Calculation of ΦMnmax (singly)
- Step No. 02: Moment to be carried by compression steel
- Step No. 03: Find εs′ and fs′
- Step No. 04: Calculation of As′ and Ast.
- Step No. 05: Ensure that d′/d < 0.2 (for grade 40) so that selection of bars does not create compressive stresses lower than yield.
- Step No. 06: Ductility requirements: Ast ≤ Astmax
- Step No. 07: Drafting
Practical Example
Design a doubly reinforced concrete beam for an ultimate flexural demand of 4500 in-kip. The beam sectional dimensions are restricted. Material strengths are fc′ = 3 ksi and fy = 40 ksi.
Step No. 01: Calculation of ΦMnmax (singly)
ρmax (singly) = 0.0203
Asmax (singly) = ρmax (singly)bd = 4.87 in2 ΦMnmax (singly) = 2948.88 in-kip
Step No. 02: Moment to be carried by compression steel
Mu (extra) = Mu – ΦMnmax (singly)
= 4500 – 2948.88 = 1551.12 in-kip
Step No. 03: Find εs′ and fs′
From table 2, d = 20″ > 12.3″, and for d′ = 2.5″, d′/d is 0.125 < 0.20 for grade 40 steel. So compression steel will yield.
Stress in compression steel fs′ = fy Alternatively,
εs′ = (0.003 – 0.008d′/d) (i)
εs′ = (0.003 – 0.008 × 2.5/20) = 0.002 > εy = 40/29000 = 0.00137
As εs′ is greater than εy, so the compression steel will yield.
Step No. 04: Calculation of As′ and Ast.
As′ = Mu(extra)/{Φfs′(d – d′)}=1551.12/{0.90×40×(20–2.5)}= 2.46 in2
Total amount of tension reinforcement (Ast) is,
Ast = Asmax (singly) + As′= 4.87 + 2.46 = 7.33 in2
Using #8 bar, with bar area Ab = 0.79 in2
No. of bars to be provided on tension side = Ast/ Ab= 7.33/ 0.79 = 9.28
No. of bars to be provided on compression side=As′/Ab = 2.46/ 0.79 = 3.11
Provide 10 #8 (7.9 in2 in 3 layers) on tension side and
4 #8 (3.16 in2 in 1 layer) on compression side.
Step No. 05:
Ensure that d′/d < 0.2 (for grade 40) so that selection of bars does not create compressive stresses lower than yield.
With tensile reinforcement of 10 #8 bars in 3 layers and compression reinforcement of 4 #8 bars in single layer, d = 19.625″ and d′ = 2.375
d′/d = 2.375/ 19.625 = 0.12 < 0.2, OK
Step No. 06: Ductility requirements:
Ast ≤ Astmax
Ast , which is the total steel area actually provided as tension reinforcement must be less than Astmax .
Astmax = Asmax (singly) + As′fs′/fy
Astmax (singly ) is a fixed number for the case under consideration and As′ is steel area actually placed on compression side.
Asmax (singly) = 4.87 in2 ; As′ = 4 × 0.79 = 3.16 in2
Astmax= 4.87 + 3.16 = 8.036 in2 Ast = 7.9 in2
Therefore Ast = 7.9 in2 < Astmax OK.
Step No. 07: Drafting
- Provide 10 #8 (7.9 in2 in 3 layers) on tension side and 4 #8 (3.16 in2 in 1 layer) on compression side.