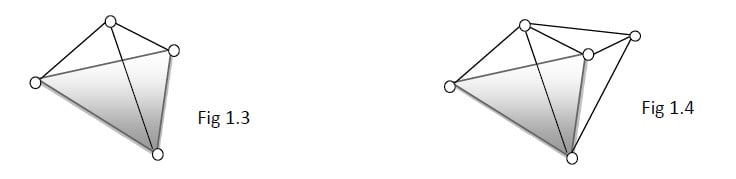Determinate and Indeterminate Structures

A structure refers to a system of connected parts used to support a load. Important examples related to civil engineering include buildings, bridges, and towers; and in other branches of engineering, ship and aircraft frames, tanks, pressure vessels, mechanical systems, and electrical supporting structures are important.

When designing a structure to serve a specified function for public use, the engineer must account for its safety, aesthetics, and serviceability, while taking into consideration economic and environmental constraints.

Idealization of the Structure

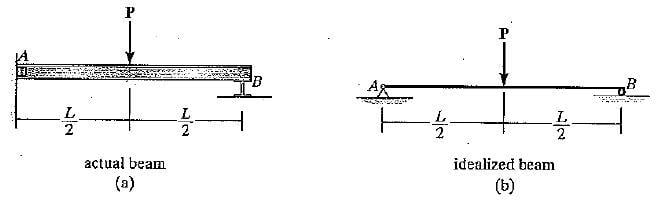
The techniques used to represent various structural systems by line drawing to analyse the structures. Idealized models used in structural analysis that represent pinned and fixed supports and pin-connected and fixed-connected joints.

Equations of static equilibrium

According to cartesian coordinate system, equations of static equilibrium are written as
ΣFx = ΣFy = ΣFz = 0 – Algebraic sums of components of all external forces along x, y and z axes = 0
ΣMx = ΣMy = ΣMz = 0 – Algebraic sums of components of all moments along x, y and z axes = 0
External forces can be divided in to two groups:

1. Applied loads,
2. Reactive forces

For the static equilibrium of plane structures three equations of equilibrium are enough to be satisfied. They are,                                                             ΣFx = 0, ΣFy= 0 and ΣMz = 0.
For the static equilibrium of space structures all the above mentioned six equations of equilibrium are to be satisfied.

Free body diagram

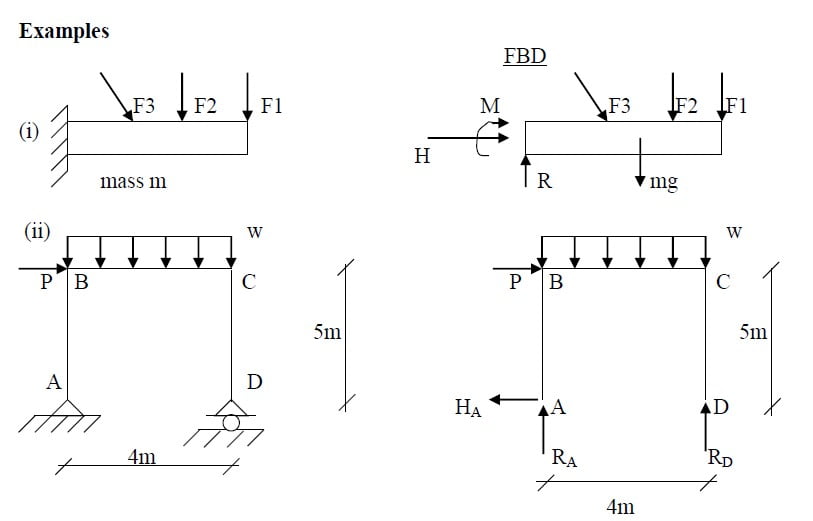
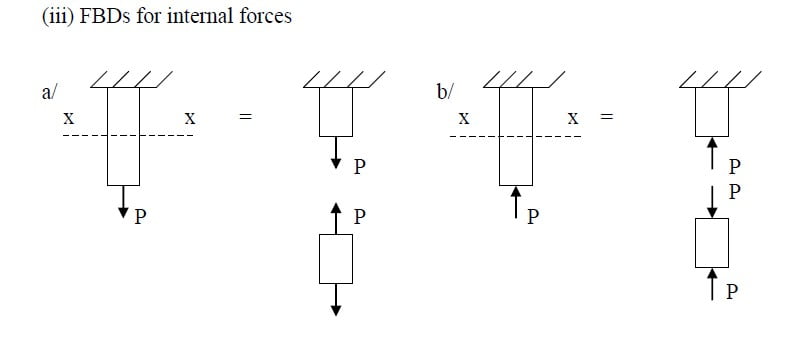
A free body diagram is a diagrammatically representation of the isolated body or combination of bodies treated as a single body, showing all forces applied to it by mechanical contact with other bodies that are imagined to be removed.
It is a concept to visualize the internal forces of a body. The free body diagram is the most important single step in the solution of problems in mechanics.

Geometric Stability & Static Determinacy and Indeterminacy of Trusses, beams and frames

Stability of structure

Stability depends on:

• Number of support reaction
• On the arrangements of the support reaction, but not depend on the strength of individual members

If the structure is said to be stable:

• Can support any possible system of applied load
• Have sufficient number of reaction to prevent motion or translation
• The arrangements of the support reaction are non-concurrent and non- parallel.

If the structure is unstable:

• Insufficient number support reaction (which means have more possibility of equation than unknown support reaction).
• The arrangements of the reaction component are concurrent and parallel

Static determinacy of structures.

• Statically indeterminate structures are those structures which cannot be analyzed with the help of equations of static equilibrium alone.
• A structure is statically indeterminate when it possesses more members or is supported by more reactive restraints than are strictly necessary for stability and equilibrium.
• In analysis of statically indeterminate structures, the number of unknowns is greater than the number of independent equations derived from the conditions of static equilibrium.
• Additional equations based on the compatibility of deformation must be written in order to obtain sufficient number of equations for the determination of all the unknowns.
• The number of such additional equations required for the determination of all the unknowns is known as the degree of static indeterminacy or degree of redundancy of the structure.

Difference between determinate and indeterminate structures

Determinacy in Truss

• The use of beams/plate-girders does not always provide the most economic or suitable structural solution when spanning large openings.
• In buildings which have lightly loaded, long span roofs, when large voids are required within the depth of roof structures for services, when plated structures are impractical, or for aesthetic/architectural reasons, the use of roof trusses, lattice girders or space-frames may be more appropriate.
• Such trusses/girders/frames, generally, transfer their loads by inducing axial tension or compressive forces in the individual members.

Degree of External indeterminacy in Truss

• External indeterminacy is related to how stably the support system exerts reaction components.
• It can be calculated as the number of external reaction components in excess of the number of equilibrium equations required for the static determinacy or minimum number of reaction components required for stability.
• A structure is usually externally indeterminate or redundant if the reactions at the supports cannot be determined by using the available equations of equilibrium.

The external indeterminacy (E) can thus be said as
Total number of reaction components (R) – minimum number of reaction components required for stability (r)

I.e. E = R – r

The degree of external indeterminacy is E = (R – 6) for space structures and E = (R – 3) for plane structures

Degree of internal indeterminacy in Truss

• Internal indeterminacy is related to the members that are more in number than that is required for stability.
• When there is more number of members in the structure, there could be more numbers of stress resultants that are unknowns to be found for the complete analysis.
• It can be said that the internal indeterminacy is based on the number of additional members present in the frame than that is required for a determinate structure, in the case of pin jointed structures and is based on the excess number of internal stress resultants in the case of rigid jointed structures.
• In a pin jointed structure the number of internal stress resultants is only one, ie either tension or compression. Hence instead of saying as number of excess stress resultants it can be said as number of excess members.

For pin jointed plane structures to be internally determinate, the equation to be satisfied is

m = 2j – 3; where m = number of members and j = number of joints.

The basic pin jointed plane internally determinate structure can be a triangular structure with 3 members and 3 joints. See fig. 1.1.

Further the pin jointed plane internally determinate structure can be created by adding 2 members and 1 joint. See fig 1.2.

Hence the equation to be satisfied for the structure to be determinate can be coined as number of members (m) = 2 times number of joints (j) – first three joints. (Of course, for the basic triangular structure, No. of members = number of joints)

The basic pin jointed space truss to be determinate should contain at least 6 members and 4 joints. See fig. 1.3. Further expansion of such determinate space truss can be done by adding 3 members and one joint. See fig. 1.4.

For the basic structure as in fig 1.3, the governing equation can be framed as m = 3j – 6.

The same equation is applicable for further addition of members and joints to form determinate space structure. The degree of internal indeterminacy in case of pin jointed structures can then be written as

I = m – (2j – 3) for plane trusses &
I = m – (3j – 6) for space trusses

Generally the degree of internal indeterminacy in case of rigid frames is determined as the number of unknown internal stress resultants minus the number of equilibrium equations.

Total degree of Indeterminacy

Total degree of indeterminacy or redundancy is equal to the number by which the unknowns (ie. Reaction components as well as stress resultants) exceed the condition equations of equilibrium. The excess restraints are called as redundant.

Determinacy of Beams

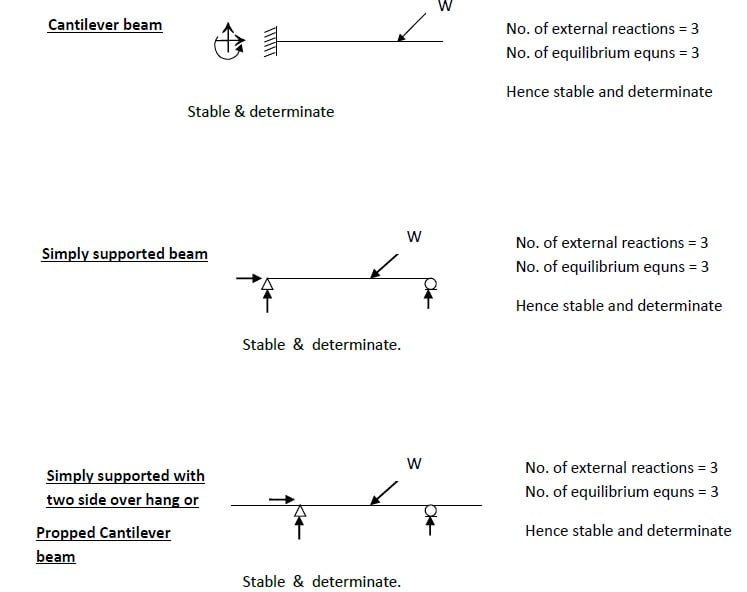
A stable structure should have at least three reactive components, but not always sufficient, for external stability of a 2D structure, which are non-concurrent and non-parallel.

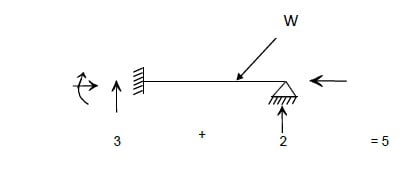
External indeterminacy in beams

Stable and indeterminate to two degrees
No. of reactions possible = 5
No. of Equations of equilibrium available = 3
Degree of External indeterminacy = 5 – 3 = 2

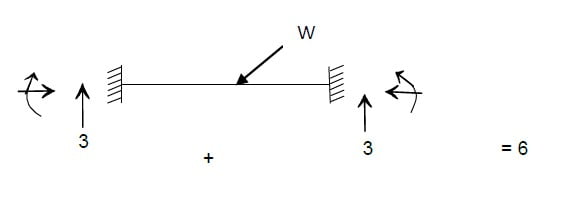
Fixed beam

Stable and indeterminate to three degrees
No. of reactions possible = 6
No. of Equations of equilibrium available = 3
Degree of External indeterminacy = 6 – 3 = 3

Simply supported beam with hinged supports

Stable and indeterminate to one degree
No. of reactions possible = 4
No. of Equations of equilibrium available = 3
Degree of External indeterminacy = 4 – 3 =1

Continuous beam

Stable & externally indeterminate to 5th degree

Determinacy of Frame

Frames are often used in building and are composed of beams and columns that are either pin or fixed connected like truss, frame s extend in two or three dimensional. The loading on a frame causes bending of its members, and if it has rigid joint connections, this structure is generally ‘’indeterminate’’ from the moment interaction between the beams and columns at the rigid joints.

Degree of indeterminacy for multi-storeyed frame

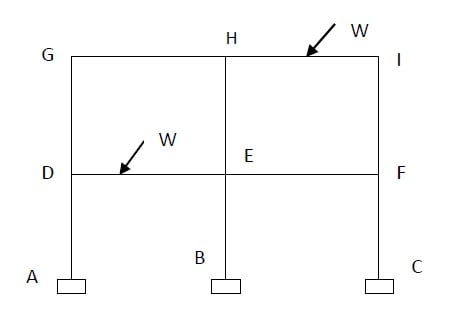
Method 1 Consider the two bay two storeyed frame shown in the fig.

External indeterminacy:

Total number of external reactions = 9

Hence the degree of external indeterminacy = R – r = 9 – 3 = 6

Internal indeterminacy:

Consider the upper storey. Let the number of vertical members in the storey be x. Number of internal reactions corresponding to x vertical members is 3x. Since three statical equations of equilibrium are available the degree of internal redundancy for this storey is

3x – 3 = 3(x – 1)

If there are n number of storeys and each storey has x vertical members, then the degree of internal redundancy would be 3(x – 1)(n – 1).

If the number of vertical members is different for different storeys, say x1 for the first storey and x2 for the second story etc.,

Total degree of internal indeterminacy = 3(x2 – 1)+3(x3 – 1)+ ….. +3(xn – 1)

= 3(x2+ x3+…..+ xn) – 3(n – 1)

(x2+ x3+…..+ xn) = Total number of columns in the upper storeys excluding the first storey.

= m (say)

Therefore degree of internal indeterminacy = 3m – 3(n – 1) = 3(m – n + 1)

In our case, m = 3, n = 2, The degree of internal indeterminacy = 3(3 – 2 + 1) = 6
Total degree of Indeterminacy = 6 + 6 = 12