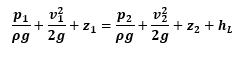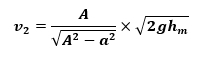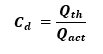For fluids, flow measurement is indispensable if we are to regulate the control processes, safety, and economy. In case of fluid discharge through a pipe, the flow quantification can be done using a number of devices one of which is a venturimeter.
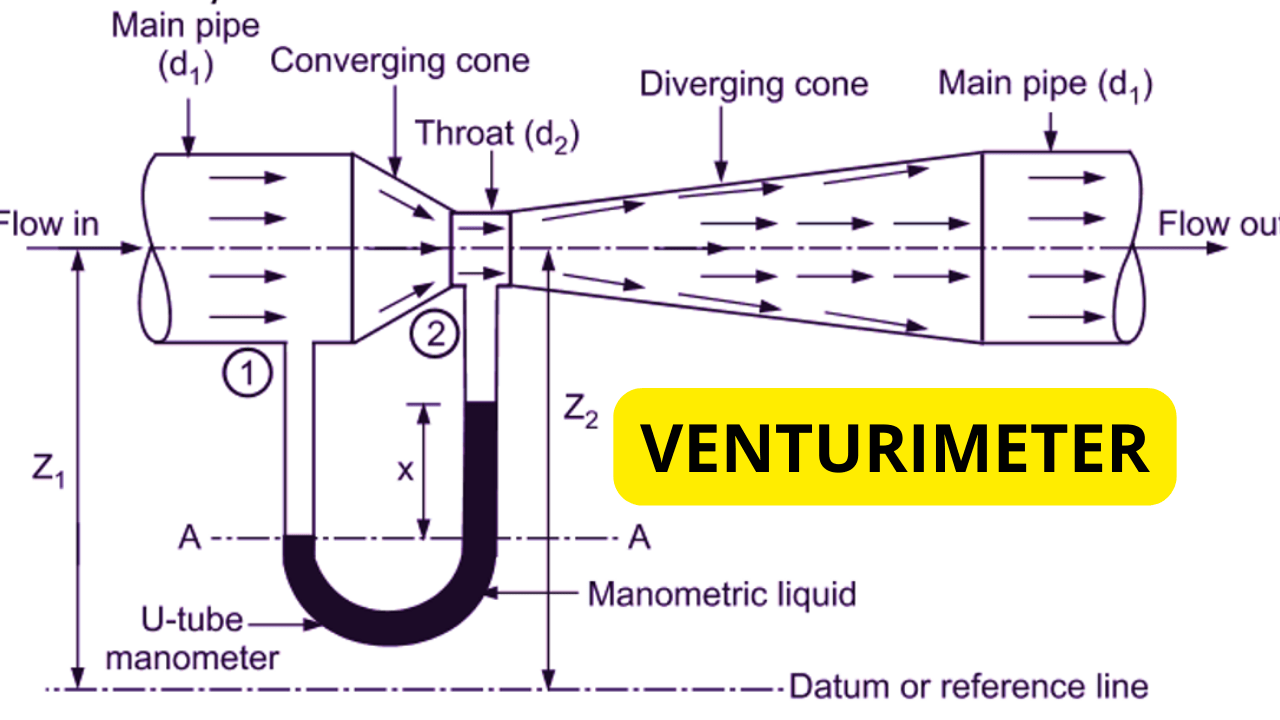
It is a non-prismatic short tube whose diameter tapers from the converging zone (or the inlet) to the throat and then from the throat to the diverging zone. A venturimeter is simply installed between any two points in a pipe and measuring the pressure head difference, it dictates the value of discharge through the pipe cross-section.
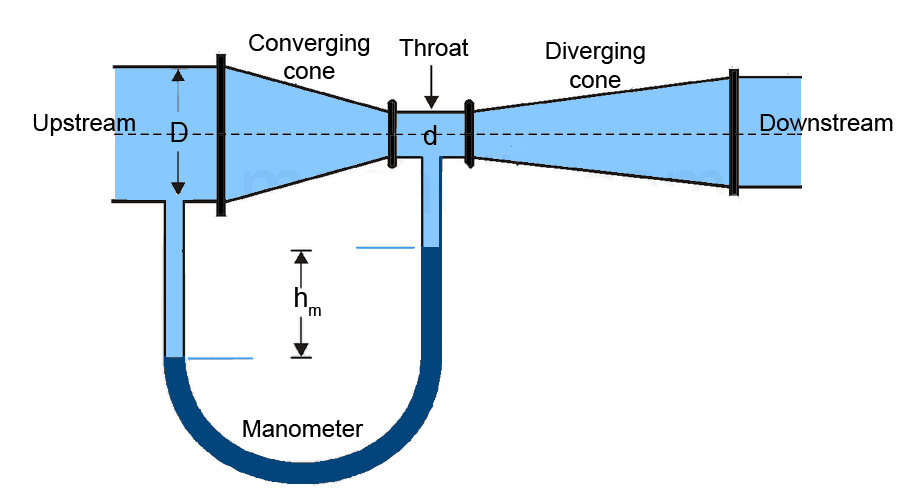
Fig.: Field venturimeter
A majority of flow measurement devices, including the venturimeter are based on Bernoulli’s equation which itself is a manifestation of the law of conservation of energy. Theoretically, the Bernoulli’s theorem holds for ideal fluids having a steady, incompressible, and irrotational fluid flow and is defined for the same as, “The total energy at any point in a fluid remains constant.”
The total energy of a fluid can be apportioned into its potential, kinetic, and pressure energies that are usually expressed in the form of the head of fluid (i.e., its energy per unit weight). Therefore, mathematically, Bernoulli’s theorem can be written as:
Where the first term on the left gives the pressure head, the second term represents the kinetic head and the last one is indicative of the potential head of fluid.
Pragmatically, the existence of such an ideal fluid is out of the question. However, the eponymous theorem can also be applied for practical fluid problems by accounting for the losses incurred in the flow. This means that for real fluids, the loss in the head is inevitable, and therefore, for any two points lying in the fluid flow path, Bernoulli’s theorem is stated mathematically as:
Where hL represents the head losses in the fluid flow from point 1 to point 2.
Table of Contents
Working of a Venturimeter
The figure shows a venturimeter fitted in a horizontal pipe containing a fluid flowing through it. It can be seen that a venturimeter consists of 3 main parts;
- A converging cone, where the area of cross-section reduces in the direction of flow and hence, the velocity surges
- A throat, where the cross-section entails the least area and the velocity hikes to the apex of its magnitude, and the pressure declines to its lowest extreme
- A diverging cone, where the cross-sectional area, as well as the pressure, are recovered with a decrement in the fluid velocity
In order to find the discharge through any pipe, it is attached between any 2 points on the pipe. The venturimeter measures the flow rate by measuring the difference in pressure heads of the fluid as it flows from the inlet towards the throat. This is given by the difference in the levels of the limbs of the manometer and knowing this, the flow rate through the pipe can be determined.
- In the figure given above, D is the diameter of the upstream end of the pipe, d is the throat diameter, and hm is the manometric head showing the difference in the pressure heads between the two sections.
- At the upstream section, the fluid has greater pressure and relatively less velocity and the left limb of the manometer depicts the same.
- This is because the cross-sectional area at this section is relatively large and the fluid pressure force pushes the manometric fluid further below. As the fluid flows towards the throat section, the area reduces, increasing the velocity of the fluid and subsequently decreasing the pressure.
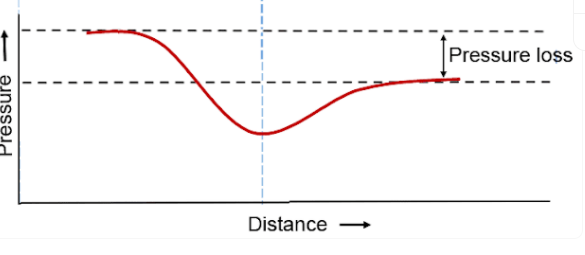
- Therefore, the right limb of the manometer shows a relatively less decrement in the depth of the manometric fluid. The adjoining figure shows the variation in pressure as the fluid flows through the venturimeter.
- It is evident from the plot that the maximum pressure decrement takes place at the throat section, after which the pressure increases but owing to head losses, the reclamation of pressure at inlet is realistically impossible.
If we apply the energy equation between the two sections, we get
Since both the sections are at the same elevation with respect to any datum, both z1 and z2 will be equal and will cancel each other from both sides of the equation. Therefore, rearranging the above equation gives,
The left-hand side of the above equation shows the pressure difference between the two sections which is equal to hm as given by the manometer.
Using the equation of continuity, Av1 = av2 where A and a are the cross-sectional areas at the inlet and throat sections respectively.
Substituting the above equation in the reduced Bernoulli’s equation and rearranging it, we get,
It is to be kept in mind that the discharge at both sections will remain the same. This is because there is a conversion of energy from one form to another between the two sections but the volume per unit time through each section of the venturimeter is the same. Therefore, Q = av2.
The above equation gives the theoretical value of discharge flowing through the pipe i.e., the flow rate under ideal conditions. The actual discharge is therefore computed as:
Where Cd is the coefficient of discharge of venturimeter.
Coefficient of Venturimeter:
For a venturimeter, the coefficient of discharge is the ratio of the theoretical discharge to the actual discharge. Mathematically,
The value of this coefficient is always less than 1.
Applications of Venturimeter
Following are some practical applications of venturimeter:
- It is used to determine the flow rate of any fluid flowing in a pipe under the influence of pressure forces. The fluids may entail gases, oils, slurries, or any other liquid (e.g., blood, water, etc.).
- It can also be used to determine the velocity of a fluid at any point in a pipe of varying cross-sections.
- For waste treatment purposes, the pipe diameters are very large. The venturimeter helps the waste particles pass through it without blocking the fluid flow.
Advantages of Venturimeter
- For flow measurement, a venturimeter can be installed in any orientation (horizontal, inclined, or vertical).
- It is easy to use as compared to the other flow measurement devices
- The coefficient of discharge of a venturimeter is greater than that of an orifice or a nozzle. This means that there is little disparity between the theoretical and experimental values of flow rate.
- The angle of convergence of a venturimeter is small. This helps in preventing excessive turbulence as the fluid velocity hikes in the converging area.
Disadvantages of Venturimeter
- A venturimeter comes in a variety of sizes, however, it is costly.
- Once it is installed, it is difficult to inspect and maintain.
- For very small diameters, a venturimeter should not be used. This is to prevent very high velocities or pressures that may have other adverse consequences.
- If any air is entrapped inside the limbs of manometer, the results may be misleading. Therefore, it must be affirmed that the limbs of the manometer are free from any ensnared air bubbles.