Physical and Thermal Properties of Aggregate and its Effect on Concrete

We have the following physical properties of concrete which have various effects on strength of concrete.

• • Specific gravity
  • Density
  • Absorption and surface moisture
  • Bulking of sand
  • Unsoundness due to volume changes

 1- Specific Gravity

• The specific gravity also called as “relative density” of an aggregate is the ratio of its weight to the weight of an equal volume of water (water displaced on immersion)

S.G = density of solid

density of water

• Depending on whether the pores are included in the measurements, we express the specific gravity in two ways:
• (i) Absolute specific gravity (ASG), and
• (ii) Bulk specific gravity (BSG), as given below

ASG = weight of aggregate (solid only) .     1    . volume of aggregate (solid only)   ^ρwater

BSG = weight of aggregate (solid +pores) .    1    . volume of aggregate (solid +pores) ^ρwater

=  weight of aggregate (solid +pores)

weight of water displaced

• The BSG volume is the realistic one to use since the effective volume that aggregate occupies in concrete includes its internal pores
• Most natural aggregates have specific gravities between 2.4 and 2.9. BSG value is used in certain computations for mixture proportioning and control

2- Density

We habe two types which are

• Bulk density
• Absolute density

(A) Bulk Density

• .”Bulk density”, also called as the unit weight, is defined as the weight per unit total volume (i.e., volume of solids + volume of voids between the particles) of aggregate

_{Bulk Density =}                    Weight                             

Volume of solids +Volume of voids

Bulk Density = Bulk Specific Gravity x 1000 kg/m³

• Bulk density of both fine and coarse normal aggregates varies within the range of 1450 to 1750 kg/m³ (90 to 110 lb/ft³)
• Bulk density is used when aggregate is to be batched by volume to convert quantities by mass to quantities by volume
• Bulk density depends on how densely the aggregate is packed (i.e. whether less or more voids) and, consequently, on the size distribution and shape of the particles
• Loose and compacted bulk densities of aggregate are determined in the laboratory
• The ratio of loose bulk density to the compacted bulk density lies usually between 0.87 and 0.96
• Knowing the bulk density (1b) and bulk specific gravity of the aggregate in SSD condition (p), the voids ratio of aggregate (e) can be calculated as:

_{e =} Volume of voids _{= 1-}          ^γb        .

Volume of solids        ρ x l000kg/m³

• Thus, the voids ratio (e) indicates the volume of mortar required to fill the space between the coarse aggregate particles. More will be the e more will be the paste requirement.
• The bulk density of the mixture of FA and CA varies with the percentage of FA in the mixture, as shown in the following figure:

• As can be observed from the above figure, the maximum bulk density of a mixture of fine and coarse aggregates is achieved when the mass of the fine aggregate is around 35 to 40% of the total mass of the mixture
• Corresponding to the maximum bulk density of a mixture of fine and coarse aggregates, there is minimum cement paste requirement (because of minimum remaining volume of voids in the mixture) and therefore there would be economy in the production of concrete

• The analysis of the mixture of FA and CA, for determination of the volume of void in the mixture (V_v) or ratio of the volume of fine aggregate to volume of coarse aggregate (V_FA/V_CA), can be carried out, as follows:

Let

V_m, V_FA, V_CA, V_v = volume of mixture, FA, CA, and voids, respectively

γ_m, γ_FA, γ_CA = bulk density of mixture, FA, and CA, respectively

We have:

V_FA+V_CA+V_v=V_m                                                                                                         Eq.l

and

W_FA+W_CA =W_m

or

γ_FA V_FA + γ_CA V_CA = γ_m V _m                                                                                          Eq.2

By solving Eq. 1 and Eq. 2, we can determine V_FA/V_CA if V_v is given, and vice-versa.

Example:-

 A mixture of sand and gravel has a unit weight of 2000 kg/m³. If the bulk specific gravity of sand is 2.3 and gravel is 2.5, and the volume percent of void ratio is 18%. Calculate the volume ratio of sand and gravel.

Explanation:-

We have,        γ_m = 2000 kg/m³

γ_FA = 2.3 x 1000 = 2300 kg/m³

γ_CA = 2.5 x 1000 = 2500 kg/m³

V_v = 18%

Considering total volume of mixtures, V_m= 1 m³

V_v = 0.18 m³

We have,       V_FA + V_CA + V_v = V_m

=>    V_FA + V_CA = 1- 0.18 = 0.82                                      (1)

Also,             γ_FA V_FA + γ_CA V_CA = γ_m V _m

2300 V_FA + 2500 V_CA=  2000

=>     2.3 V_FA + 2.5 V_CA = 2                                              (2)

By solving Eq. (1) and Eq. (2)

We get,         V_CA= 0.57 m³

and   V_FA= 0.25 m³

Ratio of sand and gravel in the mixture

= V_FA  =  0.25   =  0.438  =     1     

V_CA    0.57                       2.28

V_FA :   V_CA  =  1  :  2.28

(B) Absolute Density

• “Absolute density” is defined as the weight per unit volume of solid particles of aggregate (i.e. absolute volume) excluding the volume of voids in aggregate

_{Absolute Density =}                               Weight                    .

Volume of solids (i.e. absolute volume)

Absolute Density = Absolute Specific Gravity x 1000 kg/m³

• Absolute density is used when mix design is carried by “absolute volume method”, in which total volume of concrete is equated to the sum of absolute volumes of water, cement, aggregates, admixtures, and air.

3- Absorption and Surface Moisture  

• Due to porosity of aggregates water can be absorbed into the body of particles (Absorption), and also water can be retained on the surface of the particle as a film of moisture (Surface Moisture)
• Absorption and surface moisture both affect the w/c ratio of the concrete significantly. The absorption reduces the w/t ratio whereas surface moisture increases the w/c ratio

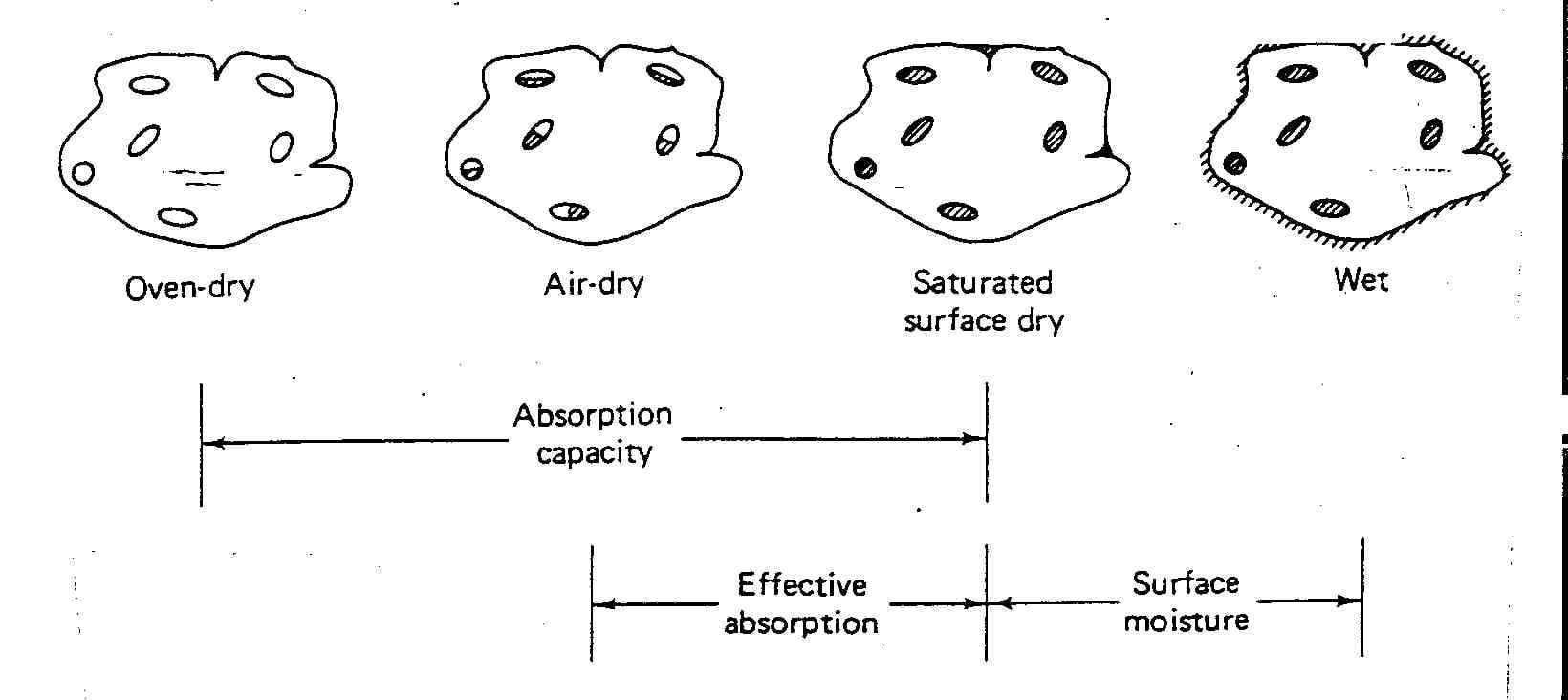
Moisture states of aggregates

Shown in the- following Fig.:

1. Oven-dry (OD): All moisture removed from the aggregate by heating in an oven at °C to constant weight (overnight heating usually suffices). All pores are empty.

2. Air-dry (AD): All moisture removed from surface, but internal pores partially full.
3. Saturated-surface-dry (SSD): All pores filled with water, but no film of water on the surface.

4. Wet: All pores completely filled with water with a film of water on the surface.

• Out of the above four states, only two, the OD and SSD states, corresponds to the specific moisture contents
• The SSD condition is the better choice as reference state, for the following reasons
• It represents the “equilibrium” moisture state of the aggregate in concrete; that is, the aggregate will neither absorb water nor give up water to the paste.
• The moisture content of aggregates in the field is much closer to the SSD state than the OD state.

The bulk specific gravity (BSG) of aggregates

It is more accurately, determined by the displacement method in the SSD condition.

• The moisture content can be calculated directly from measurements of apparent BSG using the displacement method.
• However, a major disadvantage of using the SSD is that it is not easy to obtain a true SSD condition and therefore many people prefer to use OD state as a reference point
• The expressions for calculating the absorption capacity (AC), effective absorption (EA), surface moisture (SM), and moisture contents are as follows

_{AC =}   W_SSD – W_OD  x 100%

W_OD

The absorption capacity is used in mix proportion calculations and can be converted from the SSD to OD system, or vice versa.

                                             _{EA =} W_SSD – W_AD  x 100%

W_SSD

The effective absorption is used to calculate the weight of water absorbed (W_abs) by the weight of aggregate (W_agg) in the concrete mix:

W_abs = (EA) W_agg

_{SM =} W_wet – W_SSD  x 100%

W_SSD

It is used to calculate the additional water (W_add) added to the concrete with the aggregate.

W_add = (SM) W_agg

         _{MC =} W_stock – W_SSD  x 100%

W_SSD

Where W_stock is the weight of the aggregate in the stockpiled condition. If the moisture content is positive, it is surface moisture; if negative, it is effective absorption. Thus,

W_MC = (MC) W_agg

4- Bulking

• It is the increase in total volume of moist fine aggregate over the same weight dry

Reason: Surface tension in the moisture holds the particles apart, causing an increase in volume, as shown in the following Fig.

• As shown in the above graph, the amount of bulking of FA depends on the moisture content and grading. At a same moisture content finer grading has more bulking than coarser grading
• Due to bulking the FA should not be batched by volume unless correction for the

bulking is made

5- Unsoundness due to Volume Change

• Following are the causes of unsoundness (i.e. volume changes) of aggregate:
• Freezing and thawing
• Thermal changes at temperature above freezing
• Alternate wetting and drying
• Unsoundness of aggregate result in a deterioration of the concrete in the form of local scaling (so-called pop-outs) and even extensive surface cracking

• Aggregate is tested for its unsoundness by the following methods recommended by BS and ASTM Codes:
• Alternate immersion of aggregate in sulfate solution and drying
• Subjecting the aggregate to cycles of freezing and thawing

In both methods, the unsoundness of aggregate is measured in terms of the reduction in its particle size after subjecting it to the exposures.

Thermal Properties of Aggregates

• Following are three thermal properties of aggregate relevant to the performance of concrete:
  • Coefficient of thermal expansion
  • Specific heat
  • conductivity

• Specific heat and conductivity of aggregate are of interest in mass concrete to which insulation is applied, but usually not in ordinary structural work
• The difference between coefficients of thermal expansion of aggregate and cement paste is important for the durability of concrete
• If the difference between coefficients of thermal expansion of aggregate and cement paste is smaller, durability of concrete is not adversely affected within a temperature range of 4 to 60 °C
• If the difference between coefficients of thermal expansion of aggregate and cement paste is more than 5.5 x 10^-6/^oC , durability of concrete subjected to freezing and thawing may be adversely affected
• The coefficient of thermal expansion for:
• hydrated cement paste lies between 11 and 16 x 10^-6/^oC
• rocks commonly used for aggregate lies between 5 and 13 x 10^-6/^oC