Measuring distance with the help of chain is the most common and accurate method. In this method, the horizontal or linear distances are measured with the help of chain or tape. Angular measurement is not possible by using this method of surveying. This method has widely been adapted to small plane areas with little details. This method can provide reasonable results if carefully done.
Table of Contents
Principle of Chain Surveying
Triangulation is the principle of chain surveying. Triangulation requires that the area to be surveyed should be divided into number of small triangles. These triangles should be well- conditioned in nature. Sides of triangles are directly measured on the area using chain or tape. However, there is no angular measurement done in chain surveying. Chain surveying is usually recommended when the area to be surveyed is small and it is more or less leveled.
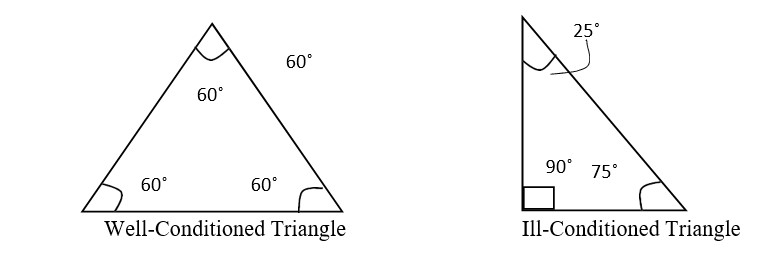
Difference between Ill-Conditioned and Well-Conditioned triangle
Well-Conditioned Triangle
Such a triangle in which all the angles are between 30˚ and 120˚.
Ill-Conditioned Triangle
Such a triangle in which an angle is less than 30˚ and more than 120˚.
Technical Terms of Chain Surveying
Base Line
The framework of the survey is built on a line that is called base line. It holds great importance in the survey. Generally, the base line is the longest of main survey lines.
Tie Line
The lines joining the tie stations are considered as tie lines. These lines are taken into account in order to fix the directions of adjacent sides of chain survey map.
Check Line
A line that joins the apex point of a triangle to some fixed point on its base is known as the check line. This line helps to locate interior details.
Main Survey Station
Stations as controlling points that are taken along the boundary of an area are known as main stations.
Tie Station
On the main survey lines there are some subsidiary stations that are known as tie stations. These stations help to locate interior details.
Offset
A lateral measurement that is taken from the object to chain line is called offset.
Methods of taking offset
There are two methods of taking offsets:
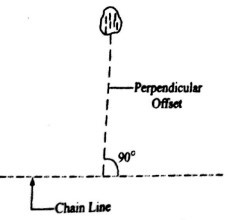
1)Perpendicular Offset
Perpendicular offset is one in which the lateral measurements are taken perpendicular to the chain line.
Fig. 1: Perpendicular Offset
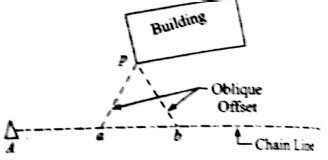
2)Oblique Offset
Any offset that is not perpendicular to the chain line is known as oblique offset.
Fig. 2: Oblique Offset
Testing of a chain
- When the chain is used continuously, it may cause some errors in the measured values during survey in field.
- A chain may be elongated or shortened, hence it is required that the chain is to be tested and adjusted accordingly. Sometimes, it is not possible to make full adjustment.
- In such case, it is necessary to note down the value of elongation or shortening, so that correction can be applied to the measured values. In order to test the chain, a test gauge is established with the help of standard steel tape on a level platform.
- The steel tape is to be standardized at 20 ˚C and under a pull of 8 kg.
- A chain is said to be in incorrect state if it gets fully stretched under a pull of normal tension i.e. 8 kg.
- Also, when the length of chain does not match with the standard length, effort should be made in order to eliminate this error. At the end, the values of elongation or shortening is noted down.
Allowable Error
20 m or 30 m
- Permissible error for 20 m chain = ±5 mm
- Permissible error for 30 m chain = ±8 m
Equipment used in Chain Surveying
Metric Chain (20 m)Cross staff or optical squarePrismatic compass with stand
| 1 no. | |
| Arrows | 10 no. |
| Metallic Tape (15 m) | 1 no. |
| Ranging Rods | 3 no. |
| Offset Rod | 1 no. |
| Clinometer | 1 no. |
| Plumb bob with thread | 1 no. |
| 1 no. | |
| 1 no. | |
| Wooden pegs | 10 no. |
| Mallet | 1 no. |
| Field book | 1 no. |
| Good pencil | 1 no. |
| Pen knife | 1 no. |
| Eraser (rubber) | 1 no. |
Procedure of Field Work
Following steps are carried out in order to conduct field work of chain survey:
1)Reconnaissance
Before starting the survey work, the surveyor should walk over the whole area to be surveyed in order to examine the ground and determine the possible arrangement of framework of survey.
The Inter-visibility of the main station should be examined by the surveyor during this investigation. The base line should preferably be takes through the center of the area and on fairly level ground.
2)Index Sketch
After reconnaissance, the arrangement of framework and approximate position of the objects is to be shown by the surveyor with the help of neat hand sketches. The base line should clearly be indicated in the index sketch.
Fig. 3: Index Sketch
3)Marking the Stations on the Ground
The stations are marked with the help of wooden pegs. These pegs are generally 2.5 cm square, 15 cm long and have pointed ends.
4)Reference Sketches
A reference sketch should be made for all the stations in order to take precaution against station pegs being missed or removed.
5)Taking Measurements of Survey Line in the Field Book
A great care should be taken while ranging and chaining to measure the distance. The magnetic bearings of base line are measured by prismatic compass. These measured values are noted down in the field book showing their offsets to the right or left according to their position in the field.
Maintaining the sequence of transverse other survey lines are ranged and chained with the help of ranging rod and chain respectively. Other related measurements are also noted down in the field book. The check lines and the lines are also measured and noted at the proper place.
Preservation of field work is to be carried out carefully so that field work is completed without any significant errors.
Uses and Applications of Chain Surveying
- It is commonly used on fairly level open land.
- It can be done for sloping ground also, but one should be vigilant to take correct values.
- It is used for planning small areas that are flat or nearly flat regions.
Problems associated with chain surveying
When the chain is too short or too long, it may cause some errors in the measured values. Following adjustments and corrections are to be made as precautionary measures in order to obtain accurate values.
Adjustment of Chain
When the chain has elongation it is adjusted by:
- Opened joints of the rings are closed.
- Elongated rings are hammered.
- Replacement of some old rings by new rings.
When the chain has shortened it is adjusted by:
- Bent links are straightened.
- Replacement of some old rings by new rings.
- Joints of the rings are opened.