Table of Contents
Objective:
The main objective of this survey job is to survey an area by chain survey across obstacles and calculate the obstructed lengths in that area.
Apparatus:
- Chain
- Fiber glass tape
- Ranging rods
- Arrows
- Cross staff
Least count of the instrument:
Least count of metric chain = 0.02 m
Least count of fiber glass tape = 0.01 m
Related theory:
Chain survey
Chain survey is the most commonly used in surveying because of its easy use. It is used in carrying out a reconnaissance survey to roughly get an idea of the site location. The chain is comprised of 100 or 150 pieces of galvanized mild steel, having a diameter of 4 mm called links.
The ends of the link are bent to shape in a loop and are connected by three oval rings. The chain ends have handles for controlling the chain on the ground. Each wire has a swivel joint so that the chain can be manipulated during its use without twisting. The length of the chain is measured between the end handles.
Types of chains
- Metric chains
- Gunter’s chain or surveyor’s chain
- Engineers chain
- Revenue chain
- Steel band or Band chain
Uses of chain survey
Uses of chain survey include:
- Reconnaissance
- Selection of station
- Length measurement
- Taking offsets
Obstacles to chaining
While surveying to take measurements, it is impossible to set out all chains in simple methods because various obstacles pose difficulty in chaining and ranging in the field. These obstacles could be of two types:
- Obstacles that do not block the view such as lakes, rivers, ponds, etc.
- Obstacles that block the view such as buildings, towers, etc.
The first type is termed as “obstacle to measurement” and the second type is called “obstacles to alignment”
Procedure:
The procedure to overcome the obstacles in chaining in the field and measure their lengths is described as follows according to each type:
1)Obstacle To Measurement:
Method-I
Suppose ABCD is a chain line blocked by a body of water such as a river or pond as shown in figure 1. BC is the obstructed length to be measured by the chain. Two offsets BE and CF having equal lengths are drawn from B and C and chaining is performed along EF to measure the distance BE. The required length of obstructed line BC is equal to the measured distance of line EF. Hence, BC = EF.
Method-Ⅱ
Assume, the blocked length across a river is AB. AC is drawn from any suitable length at a right angle to the required distance AB. Now, a perpendicular s drawn from C such that it meets the extended line of AB at D. similar triangles ABC and ADC are formed, and from the principle of similar triangles:
AB/AC = AC / AD
Hence, the required obstructed length comes out to be AB = AC2 / AD
Method-Ⅲ
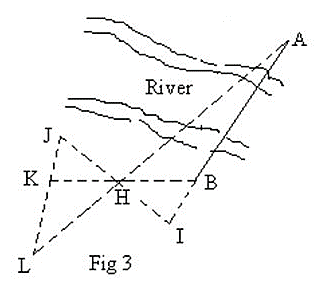
Suppose, AB is the line that is obstructed by a river body. A point I is assumed anywhere in this line with the required distance AB. A point H is taken in a way that HJ = HI and HK = HB. Now, a point L is taken in line AH and at the same time in the line, JK produced.
KHL and ABH are similar triangles and by the principle of similar triangles corresponding sides are equal to each other as the points K, B, and I, J are at equal distance from H. thus, the required length AB = KL.
2)Obstacles To Alignment
Method-I
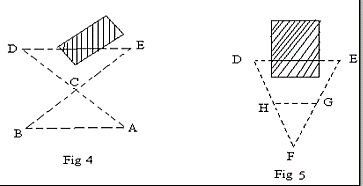
Suppose DE to be the length that is obstructed by a building as pointed in figure 4. Point C is assumed randomly. Now, E and C are joined such that EC = CB. Also, C and D are joined in a way that DC = CA. similar triangles CDE and CBA are formed and their respective sides are equal to each other as points B, E, A, and D have the same distance from C. thus, required obstructed length DE = BA.
Method-Ⅱ
In figure 5, if DE is an obstructed length across a building, then a point F is assumed equidistant from points D and E. Two more points H and G are established such that FH = FG and similar triangles FDE and FHG are formed. Using the principle of similar triangles:
DE / DF = HG / HF
Hence, obstructed length becomes DE = (HG × DF) / HF
Observations & Calculations:
1)Obstacle To Measurement:
Method-I
Measured obstructed length = (m)
Method-Ⅱ
Measured obstructed length = (m)
Method-Ⅲ
Measured obstructed length = (m)
2)Obstacles To Alignment
Method-I
Measured obstructed length = (m)
Method-Ⅱ
Measured obstructed length = (m)
Results & Discussions:
A Survey of an area by chain survey across obstacles has been performed and obstructed lengths have been calculated.
Precautions:
- The station should be marked with wooden pegs.
- Every station should be positioned with respect to three permanent points, if possible.
- Avoid trespassing personal properties and crossing busy roads.
- Establish station on firm ground.
- Run survey line parallel to the leveled ground.