Table of Contents
Related Theory
In this lab, we will study the calculation of average rainfall through different methods. To calculate the average rainfall over a catchment area, rain gauges are used to measure it. The number of gauges that needs to be installed in that area depends upon the experience of a hydrologist.
What is Precipitation?
All types of moisture reaching the surface of the earth from the atmosphere are known as precipitation. The precipitation on the land surface is about one 3rd of the total global precipitation. The precipitation on the land surface is due to 10% evaporation from the land and 90% evaporation from oceans.
Average precipitation over an area
It is the amount of precipitation that can be assumed for the entire area. One of the simplest methods is to add the precipitation of all the stations and then divide them by a number of stations in the area. The rain gauges used to measure the precipitation are shown in the figure.
Significance of Average Precipitation
If you know the average precipitation over an area then it would be very easy to compute the total volume of rainfall received by that area.
Rainfall volume = Area * Average Precipitation
Methods of Finding Average Precipitation over an area
The three most common methods are used to calculate the average precipitation of an area.
- Arithmetic mean method
- Thiessen polygon method
- Isohyetal method
Now, we shall discuss each method with their details and how can we measure average rainfall using these methods.
1)Arithmetic Mean Method
Related theory
It is the simplest method to find the average precipitation over an area. This method is applicable where precipitation gauge stations are more and have less spacing between them. This method is also used when the area is less than 500 km2.
The average precipitation over an area can be calculated as:
Where N is the total number of stations and Pi is the mean annual precipitation at the ith station.
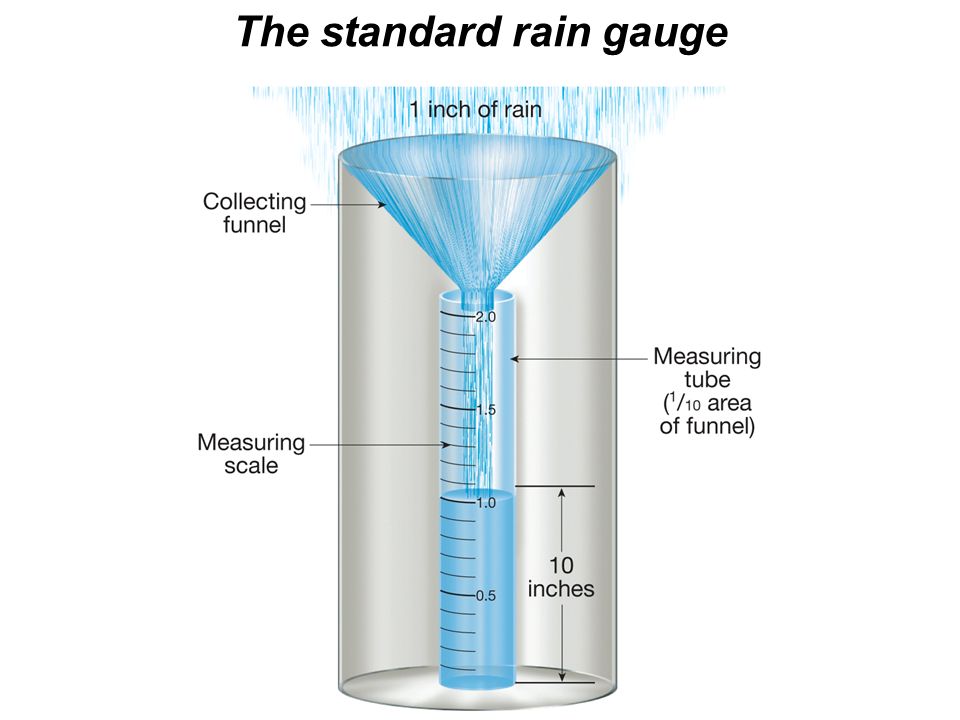
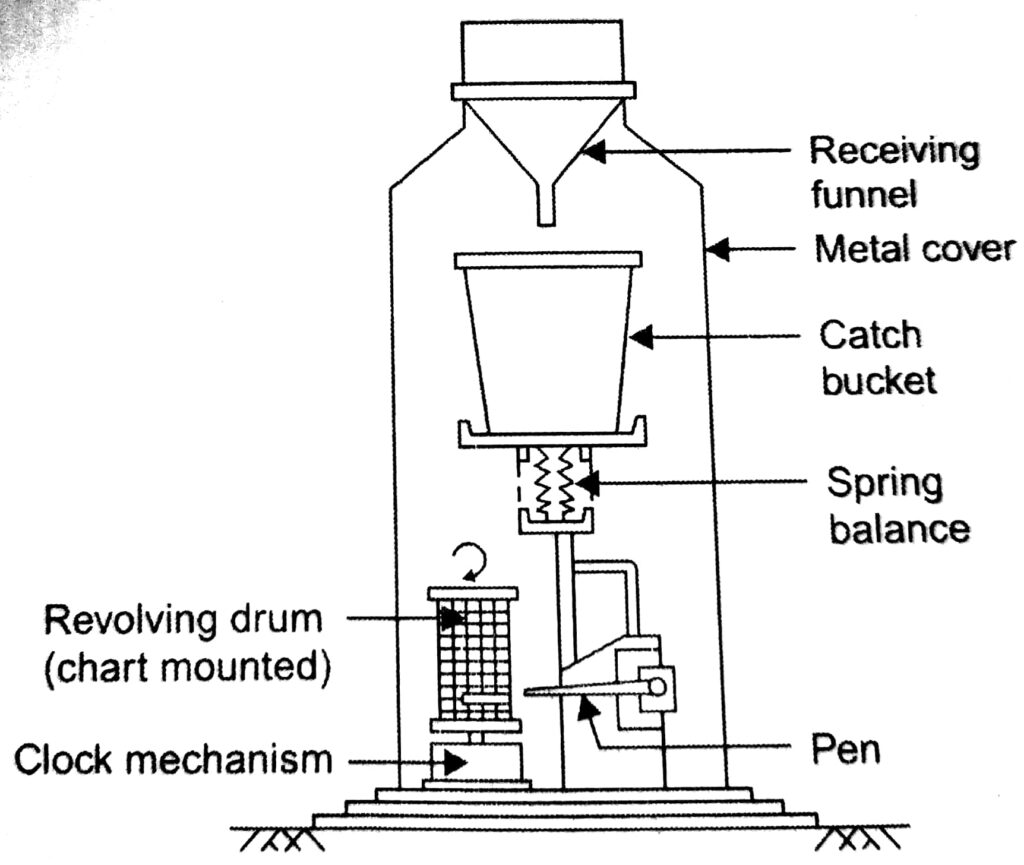
There are some different types of rain gauges that are used to measure the precipitation.
a)Standard Rain Gauge
b)Weighing bucket-type rain gauge
c)Tipping bucket-type rain gauge
Procedure
- In this method, the values of annual precipitations are collected from the different stations in that area.
- After that by taking the sum of all annual precipitations and then dividing them by the total number of stations.
- We get the value of average precipitation over that catchment area by this simplest method.
Observations & Calculations
| Station No. | Name of Station | Mean Annual PPT.
(mm) |
Average Precipitation = sum of annual precipitation / No. of stations
(mm) |
| 1 | A | ||
| 2 | B | ||
| 3 | C |
Note: this method can give accurate results if the stations over the basin are uniformly distributed.
2)Thiesen Polygon Method
Related theory
The main principle followed in this method consists of weighing the value of precipitation at each station by a suitable proportion of basin area. Then this ppt. data is plotted over a map (graph). The typical Theisen polygon graph is shown below:
 Procedure
Procedure
- Select a suitable and same scale for the X and Y-axis.
- Then plot the boundary of the catchment area and the location of each station.
- Plot polygons around each strength by connecting the closest station and then drawing the perpendicular bisectors.
- Calculate the area of each polygon by counting the number of boxes in it.
- Take the product of P1A1 and take a sum of all products.
- At the end, find the average precipitation using this formula:
Where N is the number of polygons in the catchment area, Pi is the observed annual rainfall for ith polygon and Ai is the area of ith polygon.
Observations & Calculations
| Sr. No.
(Col. # 1) |
Gauging Stations
(Col. # 2) |
Observed annual ppt., Pi (mm)
(Col. # 3) |
Area of Polygon, Ai (min2)
(Col. # 4) |
Col. 5 = col. 3*col. 4 (Pi*Ai)
(mm min2) (Col. # 5) |
| 1 | A | |||
| 2 | B | |||
| 3 | C | |||
| 4 | D |
Then by using the above formula, calculate the average precipitation over the catchment area.
Pavg = _______________________
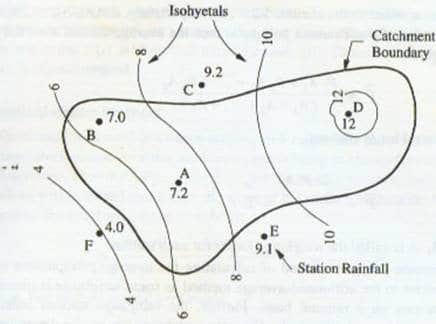
3)Isohyetal Method
Related theory
In this method, there is a line that represents the same amount of precipitations. The area between the two consecutive isohyets is determined, weighted average precipitation for each segment is computed and then average precipitation for the entire basin is determined. The typical Isohyetal map is shown below.
Procedure
- Select a suitable and same scale for the X and Y-axis.
- Then plot the boundary of the catchment area and the location of each station.
- Mention the amount of precipitation on each station.
- Select suitable contour interval and number of isohyets.
- Draw isohyets by linear interpolation between stations.
- Determine the area between two consecutive isohyets.
- Calculate the product as Pi*Ai.
- Then compute average precipitation using this formula.
Where N is the number of strips or segments in the catchment area, Pi is the mean rainfall for ith strip and Ai is the area of ith strip.
Observations & Calculations
| Sr. No.
(Col. # 1) |
Isohyetal Precipitation (mm)
(Col. # 2) |
Mean ppt. (mm)
(Col. # 3) |
Area of strip
(min2) (Col. # 4) |
Col. 5 = Col. 3 * Col. 4
(mm. min2) (Col. # 5) |
| 1 | ||||
| 2 | ||||
| 3 |
After taking the summation of column no. 4 and 5, calculate the value of average precipitation using the above formula.
Pavg = _______________________
Results and Discussions
The average annual precipitation for the watershed is:
Comparison of the results by three methods
Pavg = _______________________ (mm) by using arithmetic mean method
Pavg = _______________________ (mm) by using Thiessen Polygon method
Pavg = _______________________ (mm) by using Isohyetal method
All three methods are very useful and have a very significant role in term of computing the average precipitation. With the help of these methods we can find the average precipitation over any basin very easily and get accurate results.





 Procedure
Procedure