Compass Surveying

There are many types of surveying and compass surveying is one of them and plays an important part. We can define it as a type of surveying in which directions of survey lines are determined with help of magnetic compass and their length is measured with help of tape or chain.

To run a traverse line this type of survey is useful. The compass helps to find bearing of the lines and then obtained angle can be calculated using relevant formulas in clockwise and anti-clockwise pattern.

Figure 1: Surveying with compass                    Figure 2: Surveying Compass

History of compass surveying

Surveyor’s compass was firstly a social instrument, designed for use in places similar as Ireland and America where land was generous. The first reference to an instrument of this kind appeared in London, 1610.

Types of compass surveying

There are many types of compass but surveying compass are of four types and given below:

1. Magnetic Compass
2. GPS Compass
3. Gyro Compass
4. Astro Compass

1)Magnetic Compass

It is a compass with a magnetized needle in line with the magnetic poles of earth.

Figure 3: Magnetic Compass

A line containing magnetic bearing can be find out by this compass. Two ways to measure bearing are Whole bearing system (WBS) and Quadrantile bearing system (QBS).

Features of magnetic compass

1)Magnetic needle

To establish magnetic meridian, magnetic needle is useful.

2)Line of sight

To sight the other end of the survey line through compass we use line of sight.

3)Graduated circle

It is attached to a box or needle and helps to read the directions of the lines.

4)Compass box

In order to combine the above parts compass box is used and whole combination is then supported by means of a tripod.

Adjustments of magnetic compass

A magnetic compass must be adjusted if it shows variation more than 5^o on compass vessel. Arranging magnetic and soft iron correctors about the binnacle so their effects are equal and opposite of magnetic material in the ship are such adjustments needed for magnetic compass

Errors of magnetic compass

Magnetic compass also has some errors:

1. Variation
2. Deviation
3. Magnetic dip
4. Oscillation
5. Northerly turning error

Advantages & Disadvantages of magnetic compass

Advantages are as follows:

1. They determines true north i.e. direction of earth rotational axis.
2. They are not affected by ferromagnetic metal including iron, steel and cobalt. Disadvantages are as follows:
3. Useless at magnetic poles and unreliable in areas near it.
4. Changes readings as ships magnetic properties changes.

Types of magnetic compass

There are two further types of compasses:

• Prismatic Compass
• Surveyor’s Compass

a) Prismatic Compass

This compass is also known as Lensatic compass and is use to line up with an object whose bearing is to be determined. This prism contains a glass prism and a lid with hairline. It is often use for military purposes.

Figure 4: Prismatic compass cross section

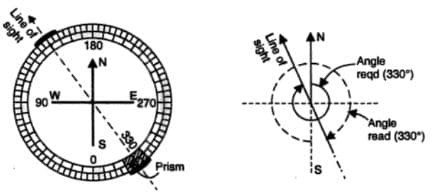
A triangular prism is attached to prismatic compass for taking more accurate readings and that’s why it is given the name prismatic compass. Bearing of lines are calculated using this compass with respect to needle. For every survey, surveyors take two bearings that are fore bearing and back bearing that should exactly vary by 180^o neglecting the minor attraction.

Figure 5: System of graduation in prismatic compass

Adjustments of Prismatic compass

1. Fixing the compass to the tripod
2. Centring the compass
3. Levelling the compass
4. Sighting the object
5. Observation of bearings

Errors of Prismatic compass

1. If plane of sight is vertical, sighting and reading errors will occur.
2. Magnetic needle must be straight neither it will give errors in readings.

Advantages & Disadvantages of Prismatic compass

Advantages are as follows:

1. They are lightweight and portable.
2. To fix it on a station they have fewer settings. Disadvantages are as follows:
3. In comparison with other surveying advance methods it is less precise and accurate.
4. Various errors like adjoining to magnetic meridian, local attraction are easily likely to occur.

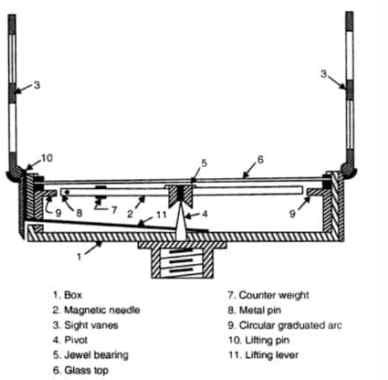
b) Surveyor’s Compass

It is a compass utilized by surveyors for motivation behind estimating horizontal angles and magnetic bearing line of sight. Its components include magnetic needle, graduated horizontal circle and sighting device. Horizontal circle is divided into 360^o. Using pair of sights we can determine the horizontal angle. There are usually adjusted on a tripod stand using ball and socket mechanism.

Figure 6: Cross section of surveyors compass

Adjustments of surveyors compass

Following are the adjustments:

1. Centering
2. Levelling
3. Focusing

Figure 7: System of graduation in surveyors compass

Errors of surveyors compass

Few errors of this compass are:

1. Local attraction (i.e. Attraction of magnetic needle to different metallic materials)
2. Improper levelling and centring of the tripod.

Advantages & Disadvantages of surveyors compass

Advantages are as follows:

1. Easy to handle.
2. Portable & Lightweight. Disadvantages are as follows:
3. It is less precise method as compare to other surveying methods
4. It is easily attracted to various errors

2)GPS Compass

GPS (Global Positioning System) compass uses satellite in geo-orbit over the earth to display exact location and direction of the motion of the target. It exactly determine the latitude, longitudes and altitudes of earth from which further calculation can be done.

Figure 8: GPS compass

Adjustments of GPS compass

If we suppose local declination is 10^o east of true north, and the waypoint is at north of your current location then:

1. If compass is being used without adjustable declination, set your GPS to magnetic north. Your GPS will display a bearing of 350^o to reach the waypoint from your current location.
2. If compass is being used with adjustable declination, set your GPS to true north. Your GPS will indicate a bearing of 0^o to reach the waypoint from your current location.

Errors of GPS compass

Major errors are:

1. Atmospheric interference
2. Calculation and rounding errors
3. Ephemeris data errors

Advantages & Disadvantages of GPS compass

Advantages are as follows:

1. Easy to handle.
2. A GPS units provides far more detailed navigational information then a compass.

Disadvantages are as follows:

1. It is less precise method as compare to other surveying methods
2. It is easily attracted to various errors

3)Gyro compass

This compass is extracted from of gyroscope and is extensively used on vessels emptying electronically powered fast spinning gyroscope wheel and other factors also like influence of graveness and earth gyration to find true north.

Figure 9: Gyro compass on ship

Adjustments of Gyro compass

It operates by searching an equilibrium direction considering the force of graveness and daily rotation of earth. It should be immune to magnetic interferences such as electric circuits.

Errors of Gyro compass

Its errors are as follows:

1. Speed error
2. Latitude error
3. Ballistic error
4. Deflection error
5. Quadrantile error

Advantages & Disadvantages of Gyro compass

Advantages are as follows:

1. It always shows true north
2. Gyro will have number of repeaters

Disadvantages are as follows:

1. It runs with electricity, when electricity fails it also fails.
2. When gyro will stop for unknown reason, it will take time to settle.

4)Astro compass

It’s a navigational tool that helps to determine true north using positions of various astronomical objects. It is used mostly for Polar Regions where magnetic and gyro compasses are not reliable. It uses current time and geographical position in form of latitude and longitude.

Figure 10: Astro compass

Adjustments of Astro compass

1. Place the compass on a tripod stand and level the device accordingly.
2. Level the compass using its levelling wheels.
3. Orient the compass to true North.

Errors of Astro compass

In order to determine the error by astronomical observation we must find true bearing of body from observer at any time. Then by comparing compass bearing with the bearing calculated, error can be extracted.

Advantages & Disadvantages of Astro compass

Advantages are as follows:

1) It shows physical relationship of the earth’s surface to the sun and is adjustable for location on earth, time of year and time of day.

Disadvantages are as follows:

1) Not in possession of nautical almanac or astronomical tables during surveying.